Introduction
Quantizing small pre-trained models at extremely low bit-widths presents a significant challenge. While we have demonstrated that larger models, like Mixtral, perform well with 2-bit quantization, smaller models, such as the popular Llama2-7B, struggle at such extreme quantization levels. Furthermore, the quality deteriorates significantly with 1-bit quantization.
The aim of this experiment is to demonstrate to the community the expected outcomes when fine-tuning such models under the most extreme quantization settings. To our surprise, fine-tuning just a fraction of the parameters (approximately 0.65%) significantly improves the output quality. Specifically, we observe that:
- 1-bit: directly applying 1-bit quantization to small models like the Llama2-7B yields suboptimal results. However, when the model is fine-tuned, its output quality improves substantially. Remarkably, the fine-tuned 1-bit base model surpasses the performance of Quip# 2-bit, despite being trained on only ~2.8K samples with a context-window of 1024.
- 2-bit: when given more specialized data, a 2-bit model can perform very well. In fact, the base Llama2-7B 2-bit model with HQQ+ outperforms the full-precision model on wikitext. The chat model outperforms its full-precision version on GSM8K when given enough math and reasoning data.
Efficient Matmul for Low-Bit Quantization
HQQ's dequantization step is a linear operation, requiring both a scaling and a zero-point parameter. We show in this section how to rewrite the dequantization step in a way to directly take advantage of extreme low-bit matrix multiplication.
Rethinking Dequantization
The dequantization step in HQQ can be expressed as \( W_{r} = (W_{q} - z)s \), where \( W_{r} \) represents the dequantized weights, \( W_{q} \) the quantized weights, and the meta-parameters \( z \) and \( s \) correspond to the zero-point and scaling factor vectors, respectively. To simplify the explanation in this article, we omit the reshaping steps that are necessary when employing grouping.
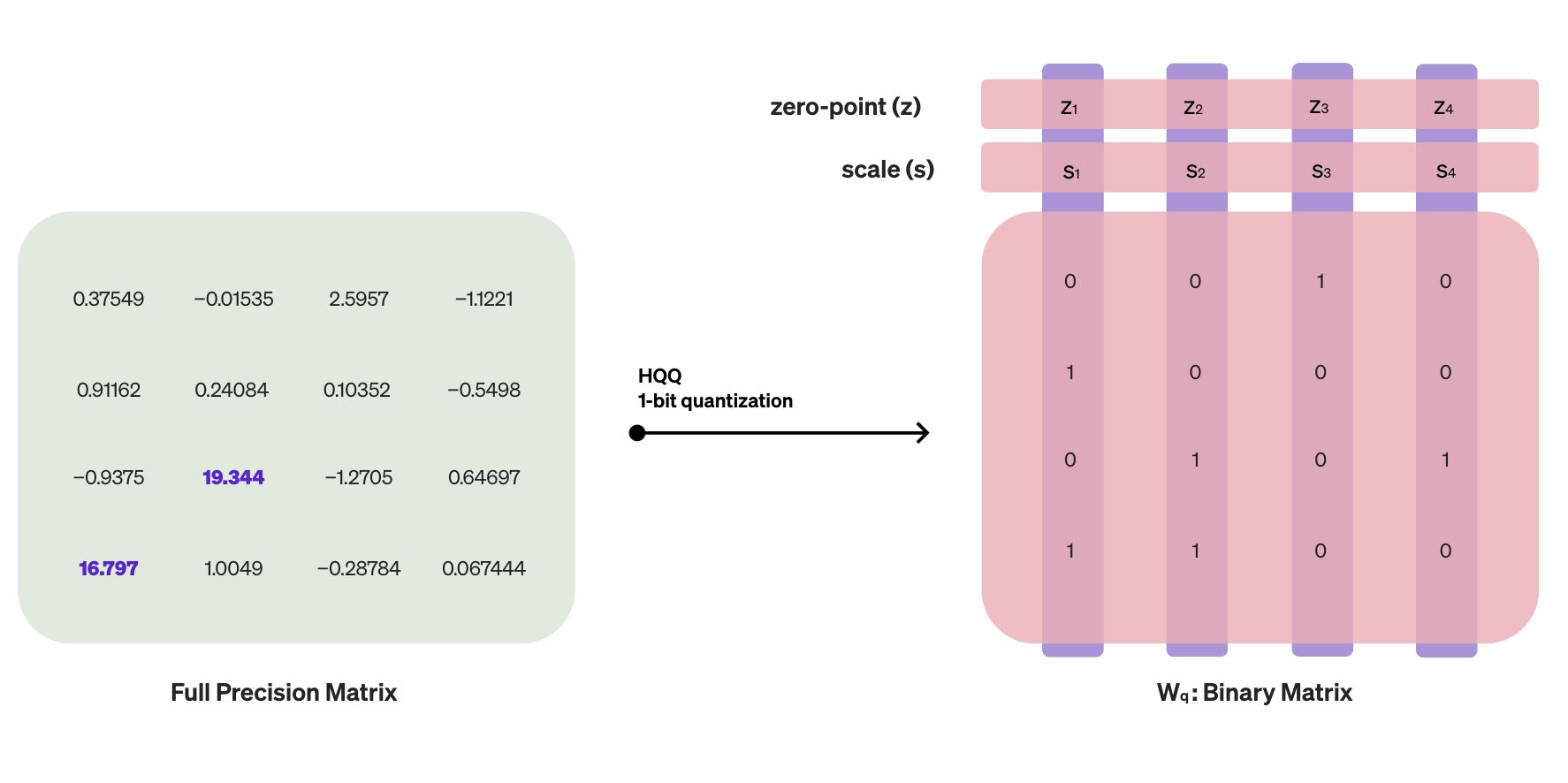
The matrix multiplication operation in the forward pass (ignoring the bias term) becomes: $$ xW_{r} = x((W_{q} - z)s). $$
To leverage the low-bit matrix multiplication, we need to separate \( xW_{q} \) from the rest. We can rewrite the operation as follows: $$ xW_{r} = x(W_{q}s + u), $$ where \( u=-z \odot s \) and \( \odot \) denotes point-wise multiplication (Hadamard product). Note that since \( u \) is a vector, we cannot directly perform matrix multiplication between \( x \) and \( u \). However, it can be formulated as a rank-1 matrix multiplication: $$ xW_{r} = x(W_{q})s + x\mathbf{1}^{T}u. ~~~~~~~~~ \style{font-size:50%}{\rm (Eq.1)} $$
In both the 1-bit and 2-bit settings, matrix multiplication with the quantized weights can be implemented as additions and does not require actual multiplication:
- In the case of binary weights, \( W_{q} \) consists of \( 0 \)s and \( 1 \)s, requiring only additions.
- In the case of 2-bit quantization, we can rewrite \( W_{q} \) as the sum of a binary and a ternary matrix, both of which can fully take advantage of multiplication-free matmul and can be implemented in a fused kernel. The only change required is to use the \([-1,0,1,2]\) range instead of the original \([0,1,2,3]\) one: $$ \underset{\text{2bit}}{\left[\begin{array}{cc} 2 & 1\\ 0 & -1 \end{array}\right]} = \underset{\text{binary}}{\left[\begin{array}{cc} 1 & 1\\ 0 & 0 \end{array}\right]} + \underset{\text{ternary}}{\left[\begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}\right]} $$
Fine-tuning with Low-Rank Adapters
Methods like BitNet train the full network from scratch. Instead, we follow the direction of training low-rank adapters (LoRA/QLoRA), which is currently the most popular way for fine-tuning large models.
As the rightmost term in Eq. 1 indicates that the zero-point acts as a rank-1 matrix error correction term between \( W_{q}s \) and the original weights, the low-rank adapter essentially increases the rank of this correction term, leading to better quantization results.
Let \({L_{A}}\) and \({L_{B}}\) be the low-rank adapter parameters of rank r, the matrix multiplication operation in the forward pass becomes:
$$ x(W_{q})s + x\mathbf{1}^{T}u + xL_{A}^{T}L_{B} $$
As detailed in our previous work on low-rank Llama pruning, the rank of the sum of two matrices is lower or equal than the sum of their ranks. Therefore, \( x\mathbf{1}^{T}u + xL_{A}^{T}L_{B} \) can be merged as a rank r+1 term to get: $$ x(W_{q})s + x\bar{L_{A}}^{T}\bar{L_{B}}, $$ where \({ \bar{L_{A}} }\) and \({ \bar{L_{B}} }\) are obtained via a low-rank decomposition of the matrix \(\mathbf{1}^{T}u + L_{A}^{T}L_{B}\).
Datasets
The low-rank adapters were trained using Supervised Fine-Tuning (SFT) on various open-source datasets. Different datasets were used for the base model and the chat model. Details are provided below:
Base Model
- wikitext-2-raw-v1 (~2.8K): This dataset was used in its entirety to fine-tune the base model, providing a foundation of general language understanding.
Chat Model
- timdettmers/openassistant-guanaco: The full dataset was utilized to fine-tune the chat model.
- microsoft/orca-math-word-problems-200k: A subset from this dataset was used to enhance the model's ability to solve mathematical word problems.
- meta-math/MetaMathQA: Another subset from this dataset was employed to further improve the model's mathematical reasoning capabilities.
- HuggingFaceH4/ultrafeedback_binarized (chosen answers only): A subset of the chosen answers from this dataset was used to fine-tune the model's ability to generate coherent and relevant responses.
In terms of subset size, we used randomly selected 10K samples for the 2-bit and 25K samples for the 1-bit model.
Benchmarks
We compared the performance of the Llama2-7B model in three configurations: FP16 (full precision), HQQ (without fine-tuning), and HQQ+ (with adapter layers) using a group-size of 8. The Llama2-7B model was chosen for these experiments because of its relatively smaller size, well-known architecture, and ease of experimentation. We evaluated the performance of both the pretrained base model and the chat model.
Base Models
For the base models, we included the results of Quip# (2-bit), a state-of-the-art quantization method by Tseng et al. We were unable to find a functioning 1-bit model other than ours for Llama-7b; however, we will include the 2-bit Quip# results as a reference.
1-bit Model
| Models | FP16 | HQQ (1-bit) | HQQ+ (1-bit) | Quip# (2-bit) |
|---|---|---|---|---|
| Wiki Perplexity | 5.18 | 9866 | 8.53 | 8.54 |
| VRAM (GB) | 13.5 | 1.76 | 1.85 | 2.72 |
| forward time (sec) | 0.1 | 0.231 | 0.257 | 0.353 |
1-bit quantization led to a significant quality loss compared to the full-precision model, rendering it almost unusable. However, with the introduction of adapter layers, the HQQ+ 1-bit model reduced its perplexity to 8.53, making it slightly better and comparable to the Quip# 2-bit model, which has a perplexity of 8.54, despite having only binary weights.
2-bit Model
| Models | FP16 | HQQ (2-bit) | HQQ+ (2-bit) | Quip# (2-bit) |
|---|---|---|---|---|
| Wiki Perplexity | 5.18 | 6.06 | 5.14 | 8.54 |
| VRAM (GB) | 13.5 | 2.6 | 2.69 | 2.72 |
| forward time (sec) | 0.1 | 0.221 | 0.27 | 0.353 |
The HQQ 2-bit model already outperforms Quip# without any calibration. After fine-tuning the adapter layers, the model remarkably achieves a lower perplexity than the full-precision model. This is a significant finding, as it suggests that quantization with HQQ+ not only reduces the memory footprint and computational requirements but can also potentially improve the model's language modeling performance.
Chat Models
For the chat models benchmark, we also include some smaller full-precision models to see how low-bit quantized models compare to smaller full-precision models.
1-bit Model
| Models | FP16 | HQQ (1-bit) | HQQ+ (1-bit) | Qwen1.5-0.5B-Chat |
|---|---|---|---|---|
| ARC (25-shot) | 53.67 | 21.59 | 31.14 | 30.55 |
| HellaSwag (10-shot) | 78.56 | 25.66 | 52.96 | 44.07 |
| MMLU (5-shot) | 48.16 | 25.08 | 26.54 | 33.82 |
| TruthfulQA-MC2 | 45.32 | 47.81 | 43.16 | 42.95 |
| Winogrande (5-shot) | 72.53 | 49.72 | 60.54 | 54.62 |
| GSM8K (5-shot) | 23.12 | 0 | 11 | 7.66 |
| Average | 53.56 | 28.31 | 37.56 | 35.61 |
The HQQ+ 1-bit model achieved an average score of 37.56 across all benchmarks, which is higher than that of Qwen1.5-0.5B-Chat (35.61). While there is still a performance gap between the 1-bit models and the FP16 model, we are optimistic of improving the performance with further fine-tuning.
2-bit Model
To further contextualize our results, we compared the 2-bit HQQ+ models with smaller language models, such as gemma-2b-zephyr-sft.
| Models | FP16 | HQQ (2-bit) | HQQ+ (2-bit) | gemma-2b-zephyr-sft |
|---|---|---|---|---|
| ARC (25-shot) | 53.67 | 45.56 | 47.01 | 49.74 |
| HellaSwag (10-shot) | 78.56 | 73.59 | 73.74 | 72.38 |
| MMLU (5-shot) | 48.16 | 43.18 | 43.33 | 41.37 |
| TruthfulQA-MC2 | 45.32 | 43.1 | 42.66 | 34.42 |
| Winogrande (5-shot) | 72.53 | 67.32 | 71.51 | 66.93 |
| GSM8K (5-shot) | 23.12 | 9.7 | 28.43 | 18.27 |
| Average | 53.56 | 47.08 | 51.11 | 47.18 |
Without any calibration, the HQQ 2-bit Llama2-7B-chat model performed very closely to the fine-tuned Gemma 2B model. The HQQ+ 2-bit model achieved an average score of 51.11, which is relatively close to the FP16 model's score of 53.56. Notably, after fine-tuning on math and reasoning data, the quantized model surpassed the FP16 model in GSM8K score, achieving 28.43 compared to 23.12. This observation raises an important question and sparks a debate about the optimal strategy for building efficient and effective language models.
A New Debate: Quantized Models or Smaller Models?
On one hand, training smaller models from scratch offers the advantage of reduced computational requirements and faster training times. Models such as Qwen1.5 have shown promising results and can be attractive options for certain applications. However, our findings indicate that heavily quantizing larger models using techniques like HQQ+ can yield superior performance while still maintaining a relatively small memory footprint.
It's important to note that these results are for Llama2-7B, which is a relatively small model. When quantized to smaller bits without an adapter layer, as in the case of vanilla HQQ, we observe high benchmark performance for larger models. For example, our previously quantized Mixtral model quantized via vanilla HQQ, demonstrates how significant memory footprint reductions can be achieved while maintaining high performance, significantly outperforming smaller models.
Conclusion
The experimental 2 and 1-bit quantized Llama2-7B models with a low-rank adapter, quantized using the proposed HQQ+ approach, showcase the potential of extreme low-bit quantization in machine learning models. Despite the challenges posed by such extreme settings, the fine-tuned models demonstrate significant improvements in output quality. We show that the fine-tuned models can take advantage of the optimized low-bit matrix multiplication formulation, which could significantly reduce the memory and compute requirements, making larger models more accessible. While binary and ternary matmul kernels are still not available, we hope this work will spark more interest to develop both software and hardware that could fully take advantage of this approach in the near future.
Citation
@misc{badri2023hqq,
title = {Towards 1-bit Machine Learning Models},
url = {https://mobiusml.github.io/1bit_blog/},
author = {Hicham Badri and Appu Shaji},
month = {March},
year = {2024}
}
