Manifold Learning has become an exciting application of geometry and in particular differential geometry to machine learning. However, I feel that there is a lot of theory behind the algorithm that is left out, and understanding it will benefit in applying the algorithms more effectively (see this).

We will begin this rather long exposition with what manifold learning is, and what are its applications to machine learning. Manifold learning is merely using the geometric properties of the data in high dimensions to implement the following things:

1. Clustering: Find groups of similar points. Given {X1,…,Xn}, build a function f : X to {1,…,k}. Two “close” points should be in the same cluster.
2. Dimensionality Reduction: Project points in a lower dimensional space while preserving structure. Given {X1,…,Xn} in R^D, build a function f : R^D to R^d where d<D. “Closeness” should be preserved.
3. Semi-Supervised, Supervised: Given labelled and unlabeled points, build a labeling function. Given {(X1,Y1),…,(Xn,Yn)}, build f : X to Y. Two “close” points should have the same label.

Where the notion of “closeness” is further refined using the distribution of the data. There are a few frameworks this is achieved with:

1. Probabilistic viewpoint: density shortens the distances
2. Cluster viewpoint: points in connected regions share the same properties
3. Manifold viewpoint: distance should be measured “along” the data manifold
4. Mixed version: two “close” points are those connected by a short path going through high density regions

The first idea we are going to cover is Laplacian Regulariation, which can be used as a regulariser in supervised and semi-supervised learning, and in dimensionality reduction by projecting onto the last eignevectors of the Laplaican.

Let us understand what Laplacian means in this context. Laplacian is merely the degree matrix (this is a measure of how many edges are incident on each vertex) minus the adjacency matrix (this is a measure how the various vertices are connected to each other). Now we are equipped to begin understanding the first method: Laplacian Regularisation

Laplacian Regularisation

Regularisation is very useful in reducing overfitting and making sure the model does not get too complex. Using the laplacian to regularise extends the idea first used in Tikhonov regularisation, which is applied to Reproducing kernel Hilbert spaces (RKHS).

We do not need to go into the nuances of RKHS, but the main result that we definitely need to understand is that in RKHS, for every function x in the function space X, there exists an unique element K_x, in the kernel, that allows us to define a norm ||f|| for every function (learned mapping function in the case of machine learning) that represents the complexity of the function in RKHS, and we can use that to regularise the algorithm. So the problem will become

This regulariser is called the extrinsic regulariser. Now laplacian regularisation adds another regulariser called the intrinsic regulariser, which consider the intrinsic geometry of the manifold and uses it to regularise the algorithm. There are several choices of how to define the regulariser, but most definitions revolve around the gradient on the manifold. We want the regulariser to penalise functions that are complicated when there is no need to be (when the data is dense). In other words, we want the function to be smooth when the data is dense, which also means that the gradient on the manifold of the function must be small when the marginal probability density of the data is large. This is formalised as

It would be awesome if we could calculate this integral directly, but as with most machine learning concepts, implementing it requires some form of estimation using the available data. In this case, we need to consider the data points as points on a graph, and connect them based on some notion of distance. This is usually done by implementing some function and imposing a condition such that if the distance (derived using the function) is less than a particular value, then the two points are connected with an edge. One such function is the standard Gaussian:

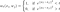
Now we need a method of estimating the integral. Going through the full derivation will make this post too long, so I shall outline the main ideas involved: using Stokes theorem and the fact that the Laplacian approximates the Laplace-Beltrami operator, we can derive an approximation to the integral for large number of data points. Therefore the regulariser can be estimated to be

Where f is the vector values of the function at the data and n is the number of data points (labelled and unlabeled). So now the final problem to be solved becomes

As with other kernel methods, the main disadvantage is that the Hilbert space might be infinite dimensional and if the regularisation cannot be found explicitly, it will be impossible to search the space for the solution. Hence, imposing certain conditions on the regularisation (strictly monotonically increasing real valued function) and using the famous Representor theorem, we can decompose the desired function into a finite dimensional space of weights alpha, such that

Now we only need to search the finite dimensional space of values for alpha to solve for the function we desire.

This is a much more complicated regularisation compared to L1 or L2 regularisation but it is very deeply involved with the geometry of the data and that seems to pay off in ensuring that the model is not overfitting.

Laplacian Eigenmap

The Laplacian eigenmap uses a similar reasoning to the above regularisation, just that it is applied to dimensionality reduction instead of regularisation. We start by generating a graph with the vertices as the data points and connects points that are a particular distance (Euclidean to be exact) and less apart. Then weights are added, usually according to the Heat kernel. Finally, eigenvalues and eigenvectors are calculated, and the data space is embedded onto a m-dimensional space using the smallest eigenvectors. Formally,

Solving this eigenvector problem

Now we can project the data onto the first m eigenvectors, f1…fm, effectively reducing the dimensions of the data.

Conclusion

To recap, we introduced what manifold learning is, where the geometry of the data is exploited to make the algorithms more efficient (either by decreasing overfitting or dimension). Next, we discussed two procedures in particular, the Laplacian regularisation and the Laplacian eigenmaps. Both of them are founded on graph theory and differential geometry and understanding the theory behind them will help in knowing when to deploy which procedure and how certain data structures can affect the efficiency of these procedures.