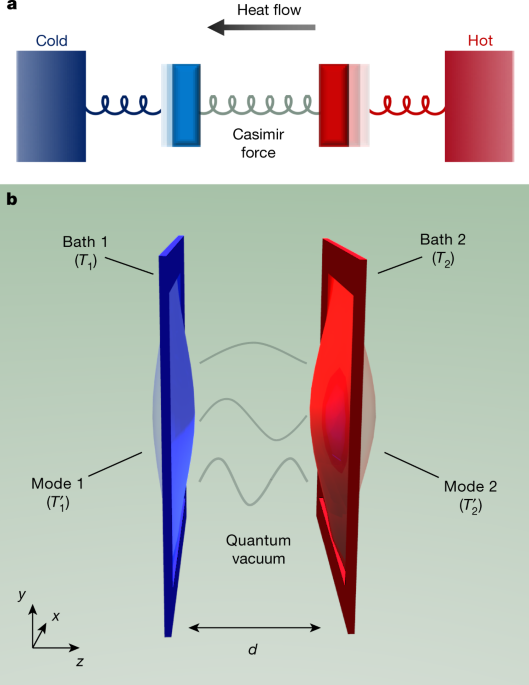
Abstract
Heat transfer in solids is typically conducted through either electrons or atomic vibrations known as phonons. In a vacuum, heat has long been thought to be transferred by radiation but not by phonons because of the lack of a medium1. Recent theory, however, has predicted that quantum fluctuations of electromagnetic fields could induce phonon coupling across a vacuum and thereby facilitate heat transfer2,3,4. Revealing this unique quantum effect experimentally would bring fundamental insights to quantum thermodynamics5 and practical implications to thermal management in nanometre-scale technologies6. Here we experimentally demonstrate heat transfer induced by quantum fluctuations between two objects separated by a vacuum gap. We use nanomechanical systems to realize strong phonon coupling through vacuum fluctuations, and observe the exchange of thermal energy between individual phonon modes. The experimental observation agrees well with our theoretical calculations and is unambiguously distinguished from other effects such as near-field radiation and electrostatic interaction. Our discovery of phonon transport through quantum fluctuations represents a previously unknown mechanism of heat transfer in addition to the conventional conduction, convection and radiation. It paves the way for the exploitation of quantum vacuum in energy transport at the nanoscale.
Access options
Subscribe to Journal
Get full journal access for 1 year
209,00 €
only 4,10 € per issue
All prices are NET prices.
VAT will be added later in the checkout.
Rent or Buy article
Get time limited or full article access on ReadCube.
from$8.99
All prices are NET prices.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- 1.
Bergman, T. L., Incropera, F. P., DeWitt, D. P. & Lavine, A. S. Fundamentals of Heat and Mass Transfer (John Wiley & Sons, 2011).
- 2.
Pendry, J. B., Sasihithlu, K. & Craster, R. V. Phonon-assisted heat transfer between vacuum-separated surfaces. Phys. Rev. B 94, 075414 (2016).
- 3.
Ezzahri, Y. & Joulain, K. Vacuum-induced phonon transfer between two solid dielectric materials: illustrating the case of Casimir force coupling. Phys. Rev. B 90, 115433 (2014).
- 4.
Budaev, B. V. & Bogy, D. B. On the role of acoustic waves (phonons) in equilibrium heat transfer exchange across a vacuum gap. Appl. Phys. Lett. 99, 053109 (2011).
- 5.
Terças, H., Ribeiro, S., Pezzutto, M. & Omar, Y. Quantum thermal machines driven by vacuum forces. Phys. Rev. E 95, 022135 (2017).
- 6.
Chiloyan, V., Garg, J., Esfarjani, K. & Chen, G. Transition from near-field thermal radiation to phonon heat conduction at sub-nanometre gaps. Nat. Commun. 6, 6755 (2015).
- 7.
Scully, M. O. & Zubairy, M. S. Quantum Optics Ch. 1 (Cambridge Univ. Press, 1997).
- 8.
Hawking, S. W. Particle creation by black holes. Commun. Math. Phys. 43, 199–220 (1975).
- 9.
Casimir, H. B. G. On the attraction between two perfectly conducting plates. Proc. K. Ned. Akad. Wet. B 51, 793–795 (1948).
- 10.
Klimchitskaya, G. L., Mohideen, U. & Mostepanenko, V. M. The Casimir force between real materials: experiment and theory. Rev. Mod. Phys. 81, 1827–1885 (2009).
- 11.
Rodriguez, A. W., Capasso, F. & Johnson, S. G. The Casimir effect in microstructured geometries. Nat. Photon. 5, 211–221 (2011).
- 12.
Lamoreaux, S. K. Demonstration of the Casimir force in the 0.6 to 6 μm range. Phys. Rev. Lett. 78, 5–8 (1997).
- 13.
Bressi, G., Carugno, G., Onofrio, R. & Ruoso, G. Measurement of the Casimir force between parallel metallic surfaces. Phys. Rev. Lett. 88, 041804 (2002).
- 14.
Chan, H. B., Aksyuk, V. A., Kleiman, R. N., Bishop, D. J. & Capasso, F. Quantum mechanical actuation of microelectromechanical systems by the Casimir force. Science 291, 1941–1944 (2001).
- 15.
Munday, J. N., Capasso, F. & Parsegian, V. A. Measured long-range repulsive Casimir–Lifshitz forces. Nature 457, 170–173 (2009).
- 16.
Garcia-Sanchez, D., Fong, K. Y., Bhaskaran, H., Lamoreaux, S. & Tang, H. X. Casimir force and in situ surface potential measurements on nanomembranes. Phys. Rev. Lett. 109, 027202 (2012).
- 17.
Somers, D. A., Garrett, J. L., Palm, K. J. & Munday, J. N. Measurement of the Casimir torque. Nature 564, 386–389 (2018).
- 18.
Altfeder, I., Voevodin, A. A. & Roy, A. K. Vacuum phonon tunneling. Phys. Rev. Lett. 105, 166101 (2010).
- 19.
Xiong, S. et al. Classical to quantum transition of heat transfer between two silica clusters. Phys. Rev. Lett. 112, 114301 (2014).
- 20.
Prunnila, M. & Meltaus, J. Acoustic phonon tunneling and heat transport due to evanescent electric fields. Phys. Rev. Lett. 105, 125501 (2010).
- 21.
Shen, S., Narayanaswamy, A. & Chen, G. Surface phonon polaritons mediated energy transfer between nanoscale gaps. Nano Lett. 9, 2909–2913 (2009).
- 22.
Ford, L. H. & Vilenkin, A. Quantum radiation by moving mirrors. Phys. Rev. D 25, 2569–2575 (1982).
- 23.
Wilson, C. M. et al. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 479, 376–379 (2011).
- 24.
Di Stefano, O. et al. Interaction of mechanical oscillators mediated by the exchange of virtual photon pairs. Phys. Rev. Lett. 122, 030402 (2019).
- 25.
Biehs, S.-A. & Agarwal, G. S. Dynamical quantum theory of heat transfer between plasmonic nanosystems. J. Opt. Soc. Am. B 30, 700–707 (2013).
- 26.
Barton, G. Classical van der Waals heat flow between oscillators and between half-spaces. J. Phys. Condens. Matter 27, 214005 (2015).
- 27.
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
- 28.
Ganjeh, Y. et al. A platform to parallelize planar surfaces and control their spatial separation with nanometer resolution. Rev. Sci. Instrum. 83, 105101 (2012).
- 29.
Błocki, J., Randrup, J., Światecki, W. J. & Tsang, C. F. Proximity forces. Ann. Phys. 105, 427–462 (1977).
- 30.
Emig, T., Hanke, A., Golestanian, R. & Kardar, M. Normal and lateral Casimir forces between deformed plates. Phys. Rev. A 67, 022114 (2003).
- 31.
Kim, W. J., Sushkov, A. O., Dalvit, D. A. & Lamoreaux, S. K. Surface contact potential patches and Casimir force measurements. Phys. Rev. A 81, 022505 (2010).
- 32.
Shen, S., Mavrokefąlos, A., Sambegoro, P. & Chen, G. Nanoscale thermal radiation between two gold surfaces. Appl. Phys. Lett. 100, 233114 (2012).
- 33.
Sushkov, A. O., Kim, W. J., Dalvit, D. A. R. & Lamoreaux, S. K. Observation of the thermal Casimir force. Nat. Phys. 7, 230–233 (2011).
- 34.
Kosloff, R. Quantum thermodynamics: a dynamical viewpoint. Entropy 15, 2100–2128 (2013).
- 35.
Vinjanampathy, S. & Anders, J. Quantum thermodynamics. Contemp. Phys. 57, 545–579 (2016).
- 36.
Luo, Y., Zhao, R. K. & Pendry, J. B. van der Waals interactions at the nanoscale: the effects of nonlocality. Proc. Natl Acad. Sci. USA 111, 18422–18427 (2014).
- 37.
Langer, G., Hartmann, J. & Reichling, M. Thermal conductivity of thin metallic films measured by photothermal profile analysis. Rev. Sci. Instrum. 68, 1510–1513 (1997).
- 38.
Zhang, X. & Grigoropoulos, C. P. Thermal conductivity and diffusivity of free-standing silicon nitride thin films. Rev. Sci. Instrum. 66, 1115–1120 (1995).
Acknowledgements
The work was supported by the National Science Foundation (NSF) under grant number 1725335, the King Abdullah University of Science and Technology Office of Sponsored Research (OSR) (award numbers OSR-2016-CRG5-2950-03 and OSR-2016-CRG5-2996); and the Ernest S. Kuh Endowed Chair Professorship.
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Tal Carmon, Karthik Sasihithlu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Numerical calculations of the Casimir force and its heat transfer effect.
a, Cross-section of the layered structure used in the experiment. b, Calculated correction factor, η, plotted against distance, d. c, Calculated coupling rate, gC, plotted against d. d, Calculated mode temperatures, \({T}_{1}^{{}^{^{\prime} }}\) and \({T}_{2}^{\text{'}}\), plotted against d on the basis of experimental condition 1 in Extended Data Fig. 2a. e, Ratio between the Casimir pressures contributed from thermal fluctuations (Fth) and quantum vacuum fluctuations (FCas) plotted against d.
Extended Data Fig. 2 Additional experimental results obtained from different samples and conditions.
a, Summary of different experimental conditions used. Condition 1 corresponds to the experimental results presented in the main text. b–f, Measurement results obtained using conditions 2 and 3. In all cases, phonon mode splitting is examined and confirms that the Casimir force is dominant over the distance range concerned. b, Resonance frequencies versus bath temperature for sample set B (conditions 2 and 3). c, d, Mode temperatures as functions of distances under different resonance-matching conditions. Error bars represent the standard error obtained from three hours of continuous measurement. e, f, Heat flux transferred across thermal baths as functions of distances. The error bars originate from error propagation in the calculation.
Extended Data Fig. 3 Electrostatic calibration of the absolute distance between membranes.
a, b, Dependence of electrostatic strength (a) and minimum splitting voltage V0 (b) on the distance between membranes. In b, the error bars represent the error of the parabolic fit to the frequency splitting versus voltage.
Extended Data Fig. 4 Near-field thermal radiation effects.
a, Frequency shifts of the two modes plotted against membrane distance. b, Frequency shifts of the two modes with the contribution from the Casimir force excluded. Measurements were carried out at bath temperatures T1 = 287.0 K and T2 = 312.5 K. The frequencies of the modes are offset by 250 Hz.
Extended Data Fig. 5 Device fabrication.
a–h, Fabrication process flow for the left (a–d) and right (e–h) samples. i, j, The left (i) and right (j) samples are attached to a custom-made copper plate and a printed circuit board, respectively.
Extended Data Fig. 6 Parallel alignment of the membranes.
a, Schematic showing the parallel alignment setup. DAQ, data acquisition system. b, c, Transmission optical images of aligned (b) and misaligned (c) membranes. d, e, Optical intensity at different locations on the membranes (marked in b, c) as a function of the change in separation. Solid lines are sinusoidal fits with an attenuation factor. The periodicity of around 230 nm matches well with the half-wavelength of the illumination light (460 nm). From the fitting, we find that the angle misalignments along the x and y directions are Δθx = 22 ± 25 μrad and Δθy = 43 ± 24 μrad for aligned membranes (d), and Δθx = 228 ± 33 μrad and Δθy = 179 ± 39 μrad for misaligned membranes (e).
Extended Data Fig. 7 Experimental setup.
a, Schematic showing the experimental setup. APD, avalanche photodetector; BS, beam splitter; DC PD, DC photodetector; L, lens; M, mirror; ND, neutral density filter. b, Optical image of the sample mount assembly and control stages.
Extended Data Fig. 8 Stability of mechanical frequency and temperature during thermal feedback.
a, Frequency stability during thermal feedback control. The shaded areas represent the linewidths of the mechanical modes. b, Bath temperatures read from the temperature controller during feedback control of the resonance frequencies.
Extended Data Fig. 9 Characterization of mechanical damping rate.
a, b, Relative change in damping rate \((\Delta {\gamma }_{i}/{\bar{\gamma }}_{i})\) plotted against distance (a) and temperature change (b). Error bars represent the standard deviation of 100 measurements.
Supplementary information
About this article
Cite this article
Fong, K.Y., Li, H., Zhao, R. et al. Phonon heat transfer across a vacuum through quantum fluctuations. Nature 576, 243–247 (2019) doi:10.1038/s41586-019-1800-4
Received
Accepted
Published
Issue Date
DOI
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.